ผมเองเป็นคนนึงที่สนใจศึกษาเรื่องของทฤษฎีเกม (Game Theory) ซึ่งเป็นทฤษฎีที่ช่วยอธิบายเรื่องการตัดสินใจเชิงกลยุทธ์ได้ค่อนข้างดี (คำว่าทฤษฎีเกมในที่นี้ไม่ได้เกี่ยวกับเกมคอมพิวเตอร์แต่อย่างใด แม้ผมจะชอบมากเหมือนกัน 555)
ดังนั้นเมื่อศึกษามาแล้วก็อยากจะลองเอามาแบ่งปันเพื่อนๆ ด้วยเช่นกัน โดยถ้าเราเอาความรู้ที่ศึกษาใหม่ มาประยุกต์กับความรู้ที่ผมมีอยู่เดิม (เช่น Excel ) แน่นอนว่ามันน่าจะช่วยให้ผมมีความเข้าใจมันลึกซึ้งมากขึ้นไปด้วย เรียกว่า Win-Win มากๆ เลยล่ะ
ก่อนที่จะลงไปใช้ Excel กับมัน แน่นอนว่าผมต้องปูพื้นฐานหลักการของทฤษฎีเกมเบื้องต้นให้ทุกคนก่อนเนอะ
สารบัญ
ทฤษฎีเกม (Game Theory) คืออะไร?
มนุษย์พยายามหาวิธีทางที่เป็นเหตุเป็นผล เป็นระบบ ในการอธิบายสถานการณ์ต่างๆ ว่ามันเกิดขึ้นได้อย่างไร? ถ้าเป็นเรื่องการทำความเข้าใจธรรมชาติเราสามารถใช้หลักการทางฟิสิกส์ เคมี ชีวะ เพื่ออธิบายสิ่งต่างๆ ได้แม่นยำมาก
แต่ถ้าพอมาเป็นเรื่องของเชิงสังคมศาสตร์ การเมือง กลยุทธ ที่เกี่ยวข้องกับการตัดสินใจของคน มันพอจะมีทฤษฎีอะไรที่จะอธิบายได้หรือไม่ว่าทำไมผลลัพธ์ถึงออกมาเป็นอย่างนั้น? ทำไมแต่ละคน แต่ละฝ่ายถึงตัดสินใจเลือก choice นั้นๆ
ข่าวดีคือ มันมีทฤษฎีที่อธิบายการตัดสินใจของคนได้ และสิ่งนั้นคือทฤษฎีเกมนั่นเอง
สรุปแล้วถ้าเอาแบบเข้าใจง่ายๆ ทฤษฎีเกมคือการวิเคราะห์สถานการณ์ที่เรียกว่าเกม (Game) ที่เกิดขึ้นระหว่างผู้เล่น (Players) สองฝ่ายขึ้นไป โดยที่แต่ละฝ่ายมีการตัดสินใจเชิงกลยุทธ์ (Strategy) โดยแข่งขันกันเพื่อให้ได้ผลลัพธ์ของเกม (Payoff) ในหนทางที่ตัวเองได้รับประโยชน์มากที่สุด
ซึ่งเกมนั้นมีหลายลักษณะ เช่น
- เกมที่เล่นพร้อมกัน (Simultaneous) vs เกมที่มีคนเล่นตามลำดับ (Sequential)
- เกมที่แข่งขันครั้งเดียว (One-shot games) vs แข่งซ้ำหลายครั้ง (Repeated games)
- ผลรางวัลรวมคงที่ (Constant sum games) หรือผลรางวัลรวมไม่คงที่ (Non-constant sum games)
คนที่เริ่มต้นพัฒนาทฤษฎีเกมขึ้นมาก็คือนักคณิตศาสตร์ที่ชื่อว่า John von Neumann และนักเศรษฐศาสตร์ที่ชื่อว่า Oskar Morgenstern ในช่วงปี 1944 แต่ว่ามันยังใช้ได้ค่อนข้างจำกัด พูดง่ายๆ คือยังไม่เจ๋งพอ
ต่อมานักคณิตศาสตร์ที่ชื่อว่า John Nash (คนเดียวกับในหนังเรื่อง Beautiful Mind นั่นแหละ) ก็นำทฤษฎีเกมมาพัฒนาต่อจนสามารถนำมาประยุกต์ใช้ได้ในหลากหลายสถานการณ์มากขึ้นจนโด่งดัง ใครสนใจเรื่อง Game Theory ก็แนะนำว่าอย่าพลาดหนังเรื่องนี้ครับ สนุกดี

วิธีการหาจุดดุลยภาพ (คำตอบ) ของเกม
ในตอนนี้ผมจะนำเสนอ 3 วิธี ดังนี้
- Iterated Elimination of Dominated Strategy คือการดูว่า มีกลยุทธใดที่ห่วยกว่ากลยุทธ์อื่นอย่างชัดเจนหรือไม่ ถ้ามีก็ตัดทิ้งไปเรื่อยๆ จนเหลือกลยุทธ์ที่เจ๋งที่สุด
- Nash Equilibrium คือ ทางเลือกที่ดีที่สุด ภายใต้กลยุทธ์ที่คู่แข่งกำลังเล่นอยู่ นั่นคือถ้าคู่แข่งเลือกทางเลือกแบบนึงไปแล้ว เราจะไม่มีแรงจูงใจในการเปลี่ยนทางเลือกไปอีกทางนึง (แม้ไม่มีกฏเกณฑ์ใดๆมาบังคับให้เราอยู่ที่เดิม) จุดนั้นแหละคือ จุดสมดุลย์ของแนช หรือ Nash Equilibrium ซึ่งก็มาจากชื่อของ John Nash นี่แหละ (ซึ่งบางเกมจะมีจุด Nash Equilibrium ได้หลายจุดนะ)
- Maximin Equilibrium คือ เลือกลยุทธที่ให้ Pay off สูงสุด จากกลยุทธที่ให้ Pay off ต่ำ นั่นคือ ให้หาค่า Min มาก่อน แล้วค่อยดูว่าค่า Min อันไหนที่มาค่ามากที่สุด (Max)
ตัวอย่างการวิเคราะห์ทางเลือกในสถานการณ์สมมติ
สมมตินาย A เลือกได้ 3 Action คือ บน กลาง ล่าง และนาย B เลือกได้ 2 Action คือ ซ้ายกับขวา ซึ่งเมื่อ Cross กันจะมีความเป็นไปได้ 3*2=6 แบบ ซึ่งได้ Pay Off หรือผลตอบแทนดังตาราง (ผสมปรับค่าในตารางให้เป็น Text ก่อนพิมพ์)
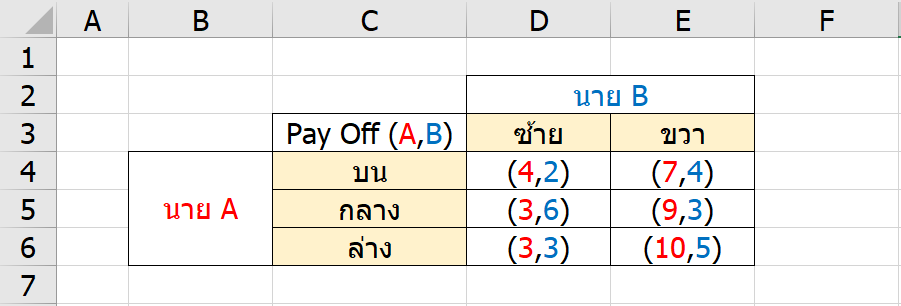
ถ้าดูผ่านๆ เหมือนว่านาย B จะเลือกยากว่าจะไปซ้ายหรือขวาดี เพราะบางกรณีซ้ายให้ผลดีกว่า บางกรณีขวาให้ผลดีกว่า ส่วนนาย A ก็ดูเหมือนจะเลือกไม่ถูกเช่นกัน เพราะบางกรณีเหมือนจะดีกว่าอีกอัน
เรามาลองวิเคราะห์ด้วยแต่ละวิธีกันว่าคำตอบจะเป็นอย่างไร?
ถ้า Solve ด้วย Iterated Elimination of Dominated Strategy (ตัดทางเลือกที่ห่วยกว่าทิ้งไปเรื่อยๆ)
จะเห็นว่า สำหรับนาย A ทางเลือกกลาง เป็นทางเลือกที่ห่วยกว่าล่างเสมอ ดังนั้นตัดทิ้ง (ด้วยการกด Hide Row/Column ใน Excel 555)
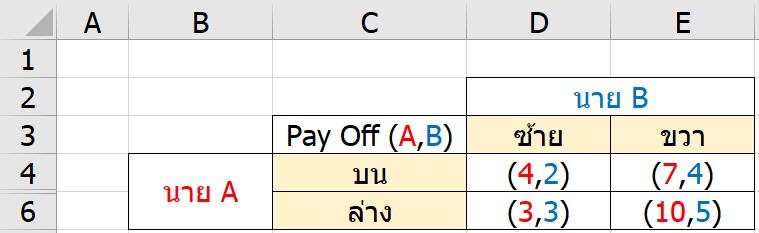
สำหรับนาย B จากสิ่งที่เหลือ ทางเลือกซ้าย เป็นทางเลือกที่ห่วยกว่าขวาเสมอ ดังนั้นตัดทิ้ง
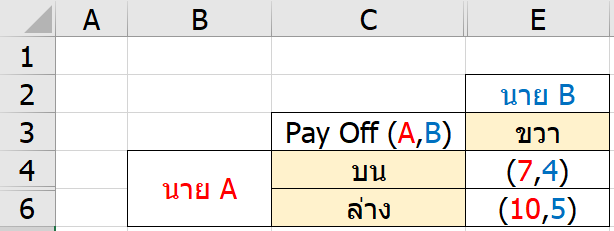
พอเห็นแบบนี้ A ก็จะต้องเลือกทางเลือกล่าง เพราะให้ผลดีกว่านั่นเอง และนี่คือคำตอบของวิธีแรกครับ

ถ้า Solve ด้วย Nash Equilibrium
ให้หาทางเลือกที่ดีสุดภายใต้ทางเลือกที่อีกคนเลือกก่อน เช่น
- สมมติให้ A เลือก บน แบบนี้ B จะเลือกขวา (เริ่มต้นที่จุดไหนก่อนก็ได้นะ)
- พอ B เลือกขวาแล้ว จะเห็นว่า A จะอยากเปลี่ยนไปเลือก ล่างแทน เพราะมันดีกว่า
- พอ B เห็น A เลือกล่างแล้ว จะพบว่าตัวเองก็อยากจะเลือกขวาอยู่ดี ไม่เปลี่ยนเป็นซ้ายแล้วเพราะมันแย่ลง
- ดังนั้นจุด ล่างขวา ก็คือ Nash Equilibrium ของเกมนี้นั่นเอง

ถ้า Solve ด้วย Maximin Equilibrium
คราวนี้ลองมาดูวิธีสุดท้ายบ้าง นั่นคือ หาค่า Payoff ที่น้อยสุดออกมาก่อน ดังนี้

จากนั้นดูว่าทางเลือกใดได้ Min Pay Off สูงสุด

ซึ่งจะกลายเป็นว่าวิธีนี้ได้ผลลัพธ์คือ บนขวา ซึ่งได้ Payoff แค่ (7,4) แทนที่จะได้ (10,5) แบบ 2 วิธีก่อน
นั่นคือ วิธี Solve อันนี้เป็นแนวทางที่ค่อนข้าง Conservative นั่นคือไม่แย่สุด แต่อาจจะไม่ได้ดีนัก ซึ่งเหมาะกับกรณีที่เราไม่มีข้อมูลคู่แข่งดีพอเป็นต้น
ตัวอย่างเคส Prisoner’s Dilemma
เคสตัวอย่างที่นิยมใช้ทฤษฎีเกมมาวิเคราะห์กันมากที่สุดและโด่งดังที่สุดก็คือ ความลำบากใจของนักโทษ (Prisoner’s Dilemma) นั่นเอง สถานการณ์คือ ตำรวจจับผู้ต้องสงสัยมาได้ 2 คน แต่หลักฐานยังไม่แน่นพอที่จะลงโทษหนักได้ (เช่น จำคุก 10 ปี) ทำได้แค่โทษเบาเท่านั้น (เช่น จำคุก 3 ปี)
ตำรวจผู้ที่รู้ซึ้งถึงทฤษฎีเกมจึงใช้แผนการจับผู้ต้องสงสัย 2 คนแยกห้องกัน และให้ข้อเสนอกับผู้ต้องสงสัยแต่ละคนว่า ถ้ายอมสารภาพจะลดโทษให้ (เช่น เหลือแค่จำคุก 1 ปี แต่ถ้าสารภาพทั้งคู่ก็จะเป็นจำคุก 5 ปี) โดยที่ผู้ต้องสงสัยแต่ละคนไม่สามารถสื่อสารกับเพื่อนได้แล้ว และไม่ค่อยมั่นใจในตัวเพื่อนเท่าไหร่ว่าจะทรยศหรือไม่?
ดังนั้นหน้าตาของตารางผลลัพธ์ของแต่ละการตัดสินใจจะเป็นแบบนี้ (ผมใส่ Pay Off ให้เป็นเลขติดลบ คือ ยิ่งจำคุกนาน ยิ่งแย่)
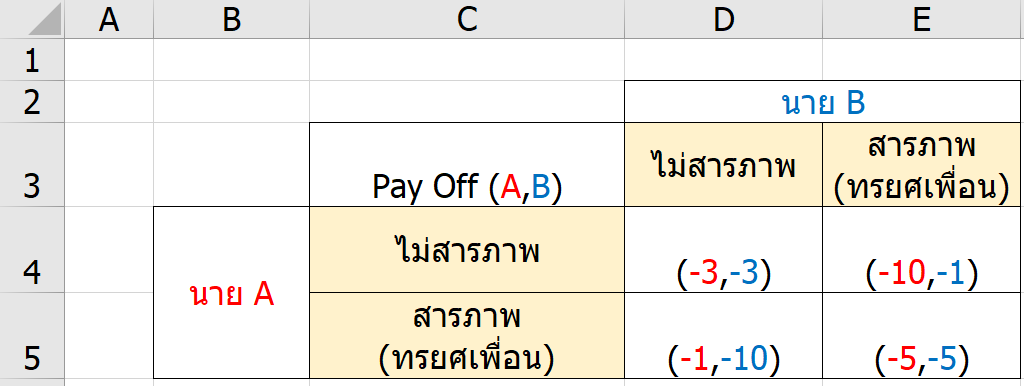
มาดูกันว่าเกมนี้ ถ้า Solve ด้วยวิธีคิดแต่ละแบบ จะให้ผลเป็นอย่างไร
ถ้า Solve ด้วย Iterated Elimination of Dominated Strategy
จะเห้นว่าทั้ง A และ B นั้น การสารภาพ(ทรยศเพื่อน) เป็นทางเลือกที่ให้ Pay Off กับตัวเองมากกว่าเสมอ ดังนั้นก็จะตัด Choice การไม่สารภาพทิ้งไปซะทั้งคู่เลย
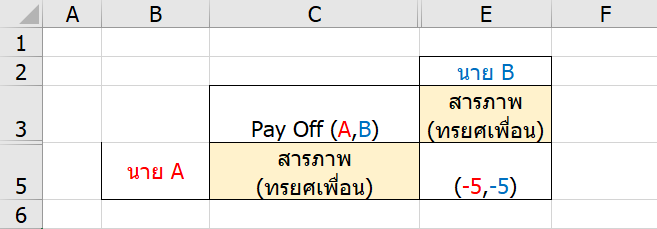
ถ้า Solve ด้วย Nash Equilibrium
- สมมติว่าเริ่มจากจุด ไม่สารภาพทั้งคู่ จะเห็นว่า B จะมีแนวโน้มอย่างเปลี่ยนเป็นสารภาพ
- พอ B อยากจะเลือกสารภาพ ทำให้ A ก็จะสารภาพด้วย
- พอสารภาพทั้งคู่ จะไม่มีใครมีความอยากที่จะเปลี่ยนการตัดสินใจแล้ว
- สรุปแล้ว จุดสมดุลของแนช คือ สารภาพกันหมดเลย

ถ้า Solve ด้วย Maximin Equilibrium
แบบนี้จะได้คำตอบเป็นสารภาพทั้งคู่เช่นกัน
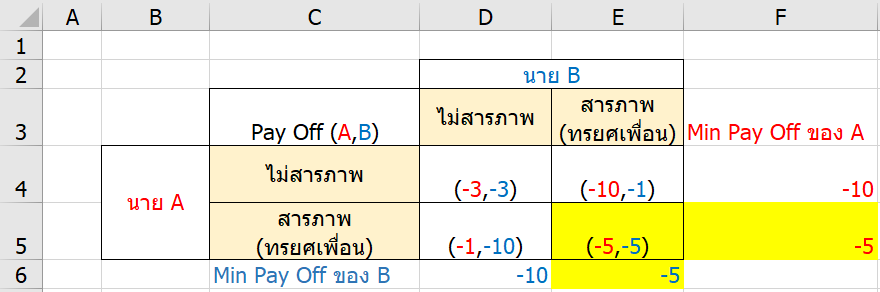
สรุป Prisoner’s Dilemma
สรุปแล้ว ทั้งนาย A และ B ตัดสินใจสารภาพทั้งคู่
กลายเป็นว่า ผลลัพธ์ของเกม ทั้งคู่ต้องถูกจำคุกคนละ 5 ปี (รวมเป็น 10 ปี) ทั้งๆ ที่ถ้าทั้งสองคนร่วมมือกันไม่สารภาพทั้งคู่ ก็จะจำคุกแค่คนละ 3 ปี (รวมเป็น 6 ปี) เท่านั้น
นี่แหละคือสิ่งที่เรียกว่า Prisoner’s Dilemma ซึ่งก็คือ สถานการณ์ที่ทำให้แต่ละคนมีแนวโน้มที่จะทรยศเพื่อเอาผลประโยชน์ของตัวเอง แต่กลับกลายเป็นว่าได้ผลลัพธ์ที่แย่กว่าการที่ทุกคนร่วมมือกัน
อย่างไรก็ตาม เคสข้างบนนี้เป็น Prisoner’s Dilemma แบบ Classic คือเล่นทีเดียวจบเลย แต่ในชีวิตจริงมันอาจจะมีเกมแบบนี้ที่เล่นได้หลายรอบกับผู้เล่นคนเดิม (เรียกว่า Iterated Prisoner’s Dilemma) ซึ่งจะทำให้มีแนวโน้มที่จะร่วมมือกันมากขึ้นเรื่อยๆ ครับ เพราะเราสามารถเรียนรู้จากการตัดสินใจของอีกคนได้ และรู้ว่าถ้าทรยศในระยะยาวจะแย่กว่าร่วมมือไปเรื่อยๆ
ตัวอย่างเคส Battle of Sexes
เป็นเกมที่ต่างฝ่ายต่างชอบเล่นกลยุทธ์คนละอย่าง แต่การเล่นกลยุทธ์แบบเดียวกัน ให้ Payoff ดีกว่าแยกกันเล่น
เช่น การเลือกว่าจะไปทำอะไรดีระหว่างคู่รักสองคน ที่ผู้ชายชอบเล่นเกม ผู้หญิงชอบดูซีรีส์ โดยที่ถ้าแฟนเราทำในสิ่งที่เราชอบก็จะฟินมาก แต่ถ้าเราทำอยู่คนเดียวจะไม่ค่อยดีเท่าไหร่ สรุปแล้ว Pay Off เป็นแบบนี้
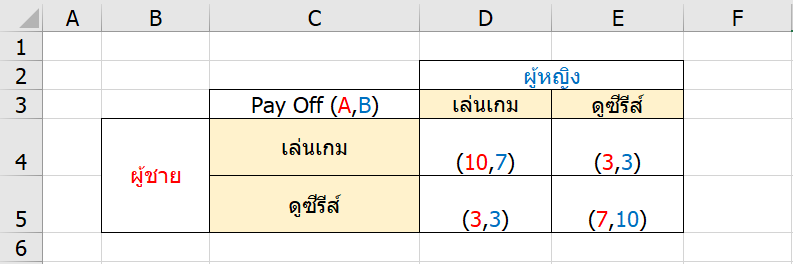
มาดูกันว่าเกมนี้ ถ้า Solve ด้วยวิธีคิดแต่ละแบบ จะให้ผลเป็นอย่างไร
ถ้า Solve ด้วย Iterated Elimination of Dominated Strategy
จะพบว่าลำดับการพิจารณาค่อนข้างมีผล คือ ถ้าผู้ชายเล่นเกม ผู้หญิงต้องเล่นเกมตาม
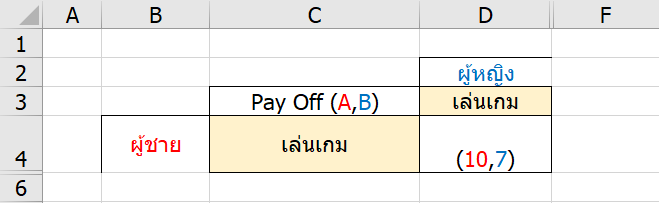
แต่ถ้าพิจารณาให้ผู้หญิงเลือกดูซีรีส์ก่อน ผู้ชายต้องดูซีรีส์ตาม
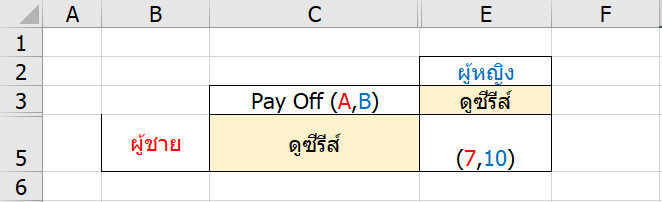
ถ้า Solve ด้วย Nash Equilibrium
จะเห็นว่าเกมนี้มีจุดสมดุลของแนชอยู่ 2 ที่ คือ เล่นเกมทั้งคู่ กับ ดูซีรีส์ทั้งคู่
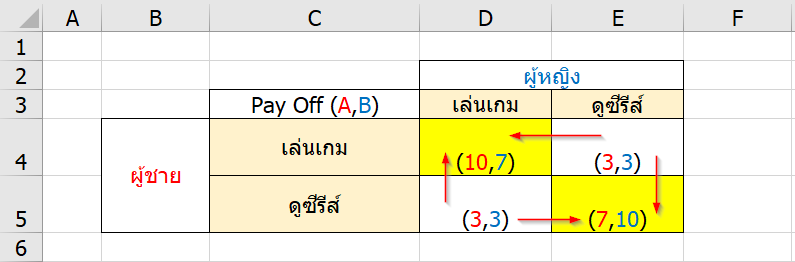
ถ้า Solve ด้วย Maximin Equilibrium

เคสนี้ไม่สามารถหาทางเลือกได้เลยเพราะคะแนนเท่ากันหมด
สรุป Battle of Sexes
ทางที่จะช่วยให้ทุกคนมีความสุขในระยะยาวคือ ให้คู่รักสลับกันเลือกสิ่งที่ตัวเองชอบนั่นเอง ดีกว่าต่างฝ่ายต่างไปทำสิ่งที่ตัวเองชอบมากกว่า โดยปราศจากแฟนเนอะ 555
จบตอนแรก
ก็จบไปแล้วกับทฤษฎีเกมตอนแรก หวังว่าจะทำให้เพื่อนๆ เห็นภาพการใช้หลักการทฤษฎีเกมเบื้องต้น และคิดว่าเนื้อหายังไม่ยากจนเกินไปเนอะ ถ้าหากอ่านแล้วสงสัยตรงไหนก็ถามได้เลยนะครับ
ใครสนใจศึกษาเพิ่มเติม ผมแนะนำ Playlist อันนี้ครับ
https://www.youtube.com/playlist?list=PLKI1h_nAkaQoDzI4xDIXzx6U2ergFmedo
ในตอนต่อไปจะเข้าสู่เนื้อหาที่ซับซ้อนมากขึ้น เช่น มีเรื่องความน่าจะเป็นมาเกี่ยวข้องด้วยครับ






Leave a Reply