ความสามารถอย่างนึงที่ Excel มีมานานมากแล้ว และทำได้ดีมากๆ ก็คือเครื่องมือ Solver ซึ่งเป็น Add-in ที่มีมาให้กับ Excel อยู่แล้วไม่ต้องไปโหลดที่ไหน (แค่ต้องกด Enable ให้มันทำงานแค่นั้น)
การใช้ Solver นั้นเหมาะกับงานที่ต้องการแก้ปัญหาในเชิง Optimization หรือหาคำตอบที่ดีที่สุดภายใต้ข้อจำกัด(หรือเงื่อนไข) ที่มีอยู่ ซึ่งเป็นอะไรที่เจ๋งมากๆ ในการทำงานจริง เพราะในชีวิตจริงเรามักจะเต็มไปด้วยข้อจำกัดเช่นกัน
และในบทความนี้ผมจะขอยกตัวอย่างการใช้ Solver ที่จะช่วยแก้ปัญหาต่างๆในการทำงานให้ เพื่อที่เพื่อนๆจะได้นำไปปรับใช้กับงานของตัวเองได้ครับ โดยมีตัวอย่างหลากหลายตั้งแต่ Product Mix, การจัดงาน, การตั้งราคา, เส้นทางการวิ่งรถ และการตัดแบ่งวัตถุดิบ บอกได้คำเดียวว่า “พลาดไม่ได้เด็ดขาด!”
สารบัญ
ขั้นตอนการใช้ Solver
การใช้ Solver นั้นมีขั้นตอนคร่าวๆ ดังนี้
- Enable Solver Add-in (ถ้ายังไม่ได้ทำ) : ให้ไปที่ File -> Excel Options -> Add-in -> Go… -> ติ๊ก Solver Addin

- เขียนสูตรผูกความสัมพันธ์ เพื่อสร้าง Model ระหว่าง Variable Input (ตัวแปรต้น) , Constrain (ข้อจำกัด) และ Objective Output (ผลลัพธ์เป้าหมาย) ที่อยากได้ให้เรียบร้อย นั่นคือ หากลองเปลี่ยน Input แล้ว Output ต้องเปลี่ยนตามอย่างถูกต้องให้ได้ซะก่อน
- เรียกใช้ Solver โดยกำหนดว่าต้องการ Maximize หรือ Minimize ค่า Objective Output โดยเลือกว่าจะให้เปลี่ยน Variable Input ตัวไหน ภายใต้เงื่อนไขของข้อจำกัด (Constrain) อะไร
หลักการทำงานของ Solver
หลักการทำงานของ Solver มันจะพยายามเปลี่ยนค่า Variable Input ไปเรื่อยๆ (สูงสุดได้ 200 Cells) ภายใต้ข้อจำกัดที่เรากำหนด เพื่อหาคำตอบว่าค่าใดทำให้เกิด Objective Output ได้ตรงตามที่เราต้องการมากที่สุด โดยที่มี Objective ได้แค่ค่าเดียวเท่านั้น (ถ้าเรามีเป้าหมายหลายอย่าง ต้องพยายามรวบเป็นค่าเดียว รวมถึงสามารถใส่ Weight ช่วยเอาได้)
เรื่องที่สำคัญ ที่หลายคนมักมองข้ามคือการเลือก Solving Method ว่าเป็นแบบใด ซึ่งเลือกได้ 3 แบบ คือ
- Simplex LP : ความสัมพันธ์ระหว่าง Input กับ Output, Input และ Constrain นั้นทุกตัวมีความต่อเนื่องกันเป็นเส้นตรง (LP=Linear Programming นั่นคือตัวแปร x ยกกำลังแค่ 1) ซึ่งรูปแบบนี้จะการันตีได้ว่า ถ้า Solver เจอคำตอบแล้วจะเป็นคำตอบที่ดีที่สุดระดับ Global แล้วจริงๆ
- GRG Non Linear : ความสัมพันธ์ระหว่าง Input กับ Output อย่างน้อยตัวใดตัวหนึ่งมีความต่อเนื่องกันแต่ไม่ได้เป็นเส้นตรง (เช่น เส้นโค้ง) ถ้าเป็นแบบนี้ อาจจะมีบางกรณีที่เส้นโค้งนั้นอาจจะหาค่าที่ดีที่สุดได้แค่ภายใต้ขอบเขต Local เท่านั้น ไม่ใช่ระดับ Global เพราะมันดันเข้าใจว่าจุดยอดเขาที่เจอคือจุดที่ Optimize แล้ว ทั้งๆ ที่จริงๆ ยังมียอดเขาที่สูงกว่าอีกยอดนึง
- วิธีทำให้ค่าที่ได้ดีขึ้นคือ ติ๊ก Option Multi Start เพื่อให้เริ่มหาที่หลายๆ จุด
- Evolutionary : ความสัมพันธ์ระหว่าง Input กับ Output อย่างน้อยตัวใดตัวหนึ่งไม่ได้มีความต่อเนื่องกัน เช่น มี IF, VLOOKUP, INDEX ทำให้ค่าผลลัพธ์หรือ Constrain เวลาคำนวณจาก Variable มันจะกระโดดไปมาได้ ซึ่งวิธีสุดท้ายนี้ผลลัพธ์จะอยู่ในระดับ Good Solution คือ ดีกว่าค่าที่ใส่ลงไปแต่แรกเท่านั้น ไม่ได้ดีในระดับ Local ด้วยซ้ำ
- วิธีที่ช่วยได้คือลอง Solve หลายๆ รอบ รวมถึงเพิ่ม Mutation Rate ใน Option เป็นต้น
ในบทความสอนการ Optimize ด้วย Calculus ผมเคยอธิบายความหมายของ Global, Local Max Min ไว้ ลองไปอ่านดูได้ครับ

ถ้าเป็นไปได้ ควรจะทำให้ Solve แบบ Simplex LP ให้ได้ เพราะมันทั้งเร็วที่สุดและได้ค่าที่ Optimize จริงๆ ถ้าใครงงและเลือกไม่ถูก ผมก็แนะนำว่าให้เลือก Simplex LP ก่อน ถ้ามัน Solve ไม่ได้ค่อยไปเลือก Non-Linear และ Evolutionary ตามลำดับครับ 555
ซึ่งขั้นตอนที่ยากที่สุดในการทำงานกับ Solver ก็คือขั้นตอนการเขียนสูตรผูกความสัมพันธ์เพื่อสร้าง Model ขั้นตอนนี้มันก็ใช้ทักษะการเขียนสูตรซึ่งก็มีทั้งยากและง่ายแล้วแต่สถานการณ์ บางทีก็เป็นแค่สูตร SUM ธรรมดา บางทีอาจจะมีเงื่อนไขมากมายทำให้ต้องมี IF, SUMIFS, SUMPRODUCT, VLOOKUP, INDEX, MATCH หรืออะไรเต็มไปหมดแล้วแต่ความซับซ้อนของ Model ที่แต่ละคนต้องทำขึ้นมา
ดังนั้นใครที่ยังเขียนสูตรไม่ค่อยเก่ง ก็จะลำบากกับขั้นตอนนี้มากหน่อย ยังไงก็ลองดูตัวอย่างที่ผมจะทำให้ดูแล้วลองเอาประยุกต์ใช้อีกทีได้นะครับ ในบทความนี้ก็จะมีให้ดูหลากหลายแบบเลยล่ะ
เพื่อไม่ให้เสียเวลาลองไปดูตัวอย่างกันเลยครับ
ตัวอย่าง 1 : Product Mix ที่ทำให้เกิดกำไรสูงสุด
ตัวอย่างนี้ผมเคยทำเป็นคลิปวีดีโอไว้ให้แล้ว เป็นตัวอย่างสุดฮิตที่เวลาสอน Solver ก็ต้องมีการพูดถึงเคสแบบนี้ นั่นก็คือ เราเป็นโรงงานผลิตสินค้า สามารถผลิตสินค้าได้หลายชนิด แต่ละชนิดก็มีกำไรต่อหน่วยต่างกัน และต้องใช้ทรัพยากรต่างกัน ทีนี้โรงงานเรามีทรัพยากรจำกัด จึงต้องคิดว่าจะใช้ทรัพยากรที่มีนั้นผลิตสินค้าอะไรบ้างอย่างละกี่ชิ้น เพื่อให้ได้กำไรสูงสุดนั่นเอง (ปัญหาแบบนี้เรียกว่า Product-Mix Problem ครับ)
Step การทำงาน
ผูกสูตร
การผูกสูตรใน Model นี้ก็ไม่มีอะไรมากไปกว่าการคูณและการบวกธรรมดาๆ แต่เพื่อให้เขียนสูตรสั้นลงเลยใช้ SUMPRODUCT มาช่วยแทนการคูณทีละคู่แล้วบวกกันแค่นั้นเอง
ตอนแรกผมใส่ Input ก็คือจำนวนที่จะผลิตมั่วๆ เป็นเลข 1,2,3 ไปก่อน เพื่อให้เห็นว่ามันสามารถคำนวณกำไรและทรัพยากรที่ใช้ไปได้อย่างถูกต้องจริงๆ
เช่นในช่องกำไรที่เขียนว่า
=SUMPRODUCT(C3:E3,C5:E5)ถ้าเขียนแบบยาวๆ ก็ต้องทำแบบนี้ ( คือ คูณกันแต่ละคู่ แล้วค่อยจับรวมกัน ซึ่งมันคือ SUMPRODUCT นั่นเอง)
=C3*C5+D3*D5+E3*E5ซึ่งช่องทรัพยกรที่ใช้ไปก็ใช้หลักการเดียวกัน ซึ่งจะได้สูตรทั้งหมดดังนี้

เรียกใช้ Solver
พอมั่นใจว่าผูกสูตรเสร็จหมดแล้วก็เรียกใช้ Solver โดยไปที่ Data -> Solver ได้เลย แล้วระบุสิ่งต่างๆ ดังนี้

- Objective (เป้าหมาย) : เป้าหมายของเราในที่นี้คือ ต้องการได้กำไรสูงสุด ดังนั้นต้องเลือกช่อง G5 (กำไร) และเลือกเป็น Max (สูงสุด) นั่นเอง
- Variable (ตัวแปรต้น) : การจะไปถึงเป้าหมายที่ต้องการนั้นต้องเปลี่ยนค่าในช่องไหน ซึ่งก็คือจำนวนที่จะผลิตนั่นเอง (C3:E3)
- Constrain (ข้อจำกัด) : ข้อจำกัดคือ ทรัพยากรที่ใช้ (F9:F11) ต้องไม่เกิน (น้อยกว่าหรือเท่ากับ) ทรัพยากรที่มีอยู่ (G9:G11) และการผลิตสินค้า ต้องมีจำนวนชิ้น (C3:E3) เป็นจำนวนเต็ม (int) เท่านั้น
Solving Method : สำหรับโจทย์ข้อแรกนั้น เราเลือก Simplex LP ได้ เพราะความสัมพันธ์ระหว่าง Objective กับ Variable และ Constrain กับ Variable นั้นเป็นเส้นตรงทั้งหมด (ตัวแปร x ทุกตัว (C3,D3,E3) นั้นยกกำลัง 1 ทั้งหมดเลย) ดังนี้ จึงควรเลือก Simplex LP นั่นเอง
- Objective กำไร = Maximize : 500C3 + 300D3 + 100E3
- แรงงาน = 12C3 + 1.5D3 + 0.5E3 <=500
- พื้นที่โกดัง = 12C3 + 8D3 + 1E3 <=2200
- เงินลงทุน = 300C3 + 150D3 + 50E3 <=70000
พอ Solve ปุ๊ปมันจะขึ้นแบบนี้ ซึ่งบอกว่า
- Solver found a solution = ได้คำตอบแล้ว
- All Constraints and Optimality conditions are satisfied. = ทำตามเงื่อนไขและ optimize ค่าได้ทั้งหมด
แถมยังมี tips บอกมาข้างล่างอีกว่า ถ้าใช้ Simplex LP แล้ว แปลว่าเจอ global optimal solution แล้วนั่นเอง

พอกด ok จะเห็นผลลัพธ์เป็นดังนี้

ซึ่งแปลว่ามันแนะนำให้ผลิต A 150 ชิ้น C 400 ชิ้น โดยไม่ต้องผลิต B เลยนั่นเอง แบบนี้จะทำให้ได้กำไรสูงสุด คือ 115,000 บาทนั่นเอง
ทีนี้ถ้าเกิดข้อมูลเปลี่ยนแปลงไป เช่น สินค้า C ใช้เงินลงทุน 100 แทนที่จำเป็น 50 ผลลัพธ์ที่ Solve ได้ก็อาจเปลี่ยนไปอีก โดยเราสามารถกดรัน Solver เพื่อ Solve ใหม่ได้เลย ไม่ต้องแก้การตั้งค่าอะไรแล้ว เพราะมันจะจำการตั้งค่าเดิมไว้ให้ สะดวกดีมากๆ

ตัวอย่าง 2 : จัดงานให้ช่าง
สมมติว่าเราเป็นผู้รับเหมา รับงานมา 5 งาน แต่สามารถส่งงานให้ช่างได้หลายคน แต่ละคนก็มีค่าจ้างต่างกัน และบางคนก็ทำงานบางงานไม่เป็นด้วย เราจะจัดงานให้ช่างยังไงเพื่อให้ต้นทุนต่ำสุด โดยที่ต้องทำงานครบทุกงาน และช่างแต่ละคนรับงานได้สูงสุดแค่ 2 งานเท่านั้น (ซึ่งปัญหาแนวนี้เรียกว่า Assignment Problem ครับ)
โดยที่ค่าจ้างช่างสำหรับแต่ละงานเป็นดังนี้

เราจะสร้างตาราง Variable ขึ้นมาอีกตารางนึง ว่าจะจ้างช่างสำหรับงานนั้นๆ หรือไม่ ถ้าจ้างจะเป็นเลข 1 ไม่จ้างเป็นเลข 0 เพื่อที่จะเอา 2 ตารางคูณกัน และนำมาบวกกันให้ได้ต้นทุนรวม
นอกจากนั้นเราทำการคำนวณจำนวนงานรวมของแต่ละแถวออกมา เพื่อจะได้ใส่เงื่อนไขว่าไม่เกิน 2 (ช่าง 1 คนรับได้สูงสุด 2 งาน) และจำนวนงานรวมของแต่ละคอลัมน์ว่าจะต้องเป็น 1 (แต่ละงานทำแค่ 1 คน)

ทีนี้ถ้าเราเอา Model นี้ไปรัน Solver เลยตรงๆ เราต้องมานั่งเล็ง Variable Input โดยหาทางเว้นงานที่ช่างบางคนทำไม่เป็นอีก (ที่เป็นตัว x) ซึ่งจะยุ่งยากมาก ดังนั้นเราจึงมี Trick ในการทำคือ ให้ใส่ Cost ในงานที่ทำไม่เป็นไปสูงๆ เลย เช่น เลข 99999 Solver จะได้ไม่เลือกทำงานนั้นให้เรา
ดังนั้น Model จะออกมาเป็นดังนี้

ทีนี้ก็เรียกใช้ Solver โดยที่
- Objective : เราต้องการต้นทุนต่ำสุด คราวนี้จึงต้องเลือก Min ช่อง H3
- Variable : ช่องที่จะให้ Solver เปลี่ยนค่าเล่นได้ คือ B13:F19
- Constrain :
- ผลรวมแต่ละคอลัมน์ (B20:F20) เป็น 1
- ผลรวมแต่ละแถว (G13:G19) ไม่เกิน 2
- ค่า Variable B13:F19 เป็น Binary (Bin) คือได้แค่ค่า 0,1 เท่านั้น
- Solving Method : เป็น Simplex LP เนื่องจากสมการเป็นเส้นตรงทั้งหมดเช่นเดิม
- เช่น ต้นทุนรวม = 1300B13+1200C13+1300D13+2100E13…. ไปเรื่อยๆ ทุกตัวเป็นกำลัง1 หมด
- ข้อจำกัด เกิดจาก B13+C13+D13+E13… <=2 ทุกตัวก็กำลัง 1 หมด
สรุปเลือกดังนี้


กำหนดเงื่อนไขของช่างแต่ละคน งานแต่ละงาน
ถ้าหากช่างแต่ละคน Capacity ไม่เท่ากัน ก็อาจกรอกค่า Capacity เอาไว้ในตารางได้ เช่น ให้กด Change ที่ Constrain เดิม โดยเปลี่ยน Constraint จากเลข 2 เป็น Capacity ที่เตรียมไว้นั่นคือ H13:H19 ได้เลย
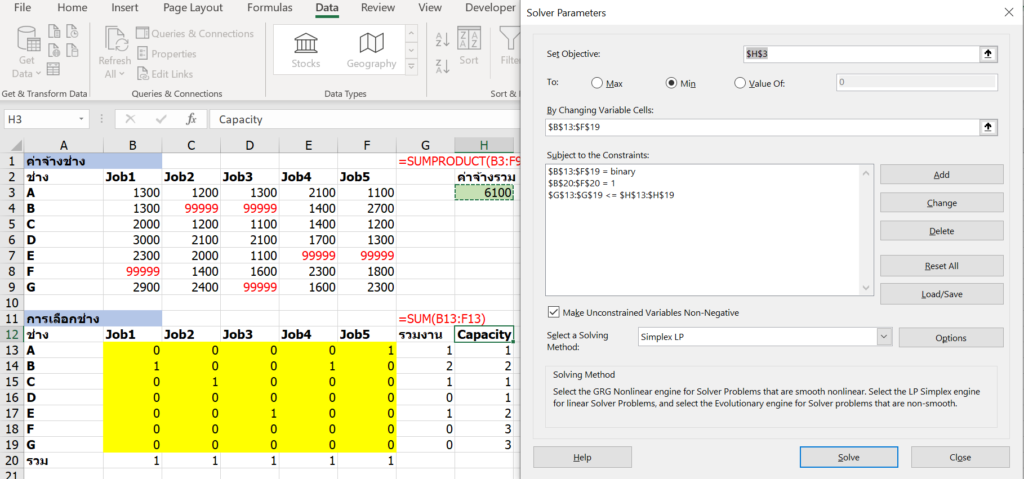
ถ้างานแต่ละงานต้องการจำนวนช่างไม่เท่ากัน ก็ระบุเงื่อนไขได้คล้ายๆ กับเรื่องของ Capacity เลย ง่ายมั้ยล่ะ!

ตัวอย่าง 3 : การตั้งราคาสินค้า
สมมติว่าเราเป็นบริษัทที่มีผลิตภัณฑ์อยู่ 2 ตัว เป็นสินค้าประเภทเดียวกันแต่เป็นรุ่นเล็กกับรุ่นใหญ่ การตั้งราคาตัวนึงจะส่งผลไปที่ราคาอีกตัวนึงได้ด้วย
จากการวิจัยพบว่าความสัมพันธ์ระหว่าง ราคาต่อหน่วย และปริมาณที่จะขายได้ของผลิตภัณฑ์แต่ละตัวเป็นดังนี้
- Q1 = 1000-2P1+1.2P2
- Q2 = 3000+0.1P1-0.5P2
เราอยากรู้ว่าตั้งราคาสินค้าทั้งสองตัวนี้เป็นเท่าไหร่ดีจึงจะได้ผลกำไรสูงสุด โดยที่ปัจจุบันตั้งอยู่ที่ P1=1500 และ P2=5000 ตามลำดับ
ซึ่งเราจะเขียน Model คำนวณรายได้รวมออกมาได้ดังนี้

นอกจากนี้หากเราอยากให้ปริมาณออกมาเป็นบวกเสมอ ก็ใส่ Constrain เข้าไปได้ ส่วนราคาถ้าอยากได้จำนวนเต็มก็ใส่เงื่อนไขเข้าไปได้เช่นกัน

แต่ข้อนี้หาก Solve ด้วย Simplex LP เหมือนเดิมมันจะไม่ยอมแล้ว

หากติ๊กที่ Linearity Report แล้ว Ok จะเห็นว่าปัญหาอยู่ที่ไหน
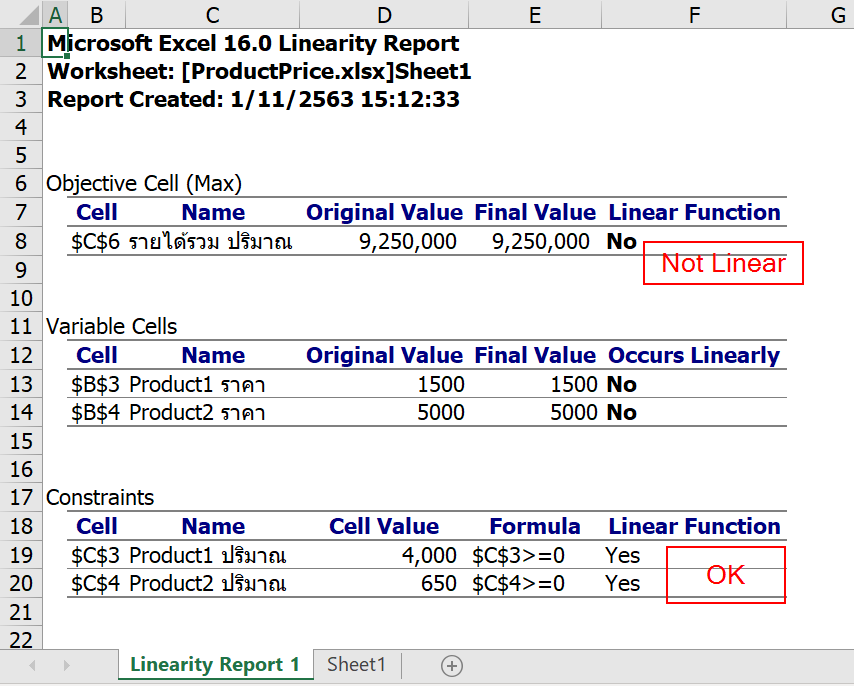
ที่สมการที่เราคิดรายได้รวมไม่ใช่ Linear เพราะมันเกิดจากการเอาราคาไปคูณปริมาณ ซึ่งปริมาณดันคำนวณมาจากราคาอีกทีนึงด้วย ทำให้เกิด Term ที่เป็นราคากำลังสองขึ้นมานั่นเอง
ดังนั้นในข้อนี้เราต้องแก้ Solving Method เป็น GRG Nonlinear แล้วค่อย Solve ครับ

จะเห็นว่าคราวนี้ผลลัพธ์ออกมาได้รายได้มากกว่าเดิมเยอะเลย เวลาใช้งานจริงๆ ก็ไม่ต้องใช้เลขราคานี้เป๊ะๆก็ได้ แต่น่าจะเห็นแนวทางแล้วนะครับ
หรือถ้าเรามีเงื่อนไขอะไรเพิ่มอีก ก็ใส่ไป เช่น ราคา Product1 ห้ามเกิน 2000 ไม่งั้นแพงไป ก็แค่ใส่ Constrain เพิ่มไปเลยครับ

ตัวอย่าง 4 : จัดเส้นทางการเดินรถโดยที่ต้นทุนต่ำสุด
สำหรับตัวอย่างนี้จะเป็นเรื่องของการ Optimize เส้นทางการเดินรถเพื่อให้พนักงานขายเดินทางไปเยี่ยมลูกค้า โดยรู้ตำแหน่งของลูกค้าแต่ละเจ้าว่าอยู่พิกัดไหน สิ่งที่เราต้องการคือ หาเส้นทางการวิ่งรถโดยที่ใช้ระยะทางการวิ่งที่น้อยที่สุด เพื่อทำให้ Cost ต่ำสุดนั่นเอง ปัญหาแบบนี้มีชื่อภาษาอังกฤษเรียกว่า Travelling salesman problem
สมมติว่าพิกัดทั้ง 10 ตำแหน่งเป็นดังนี้
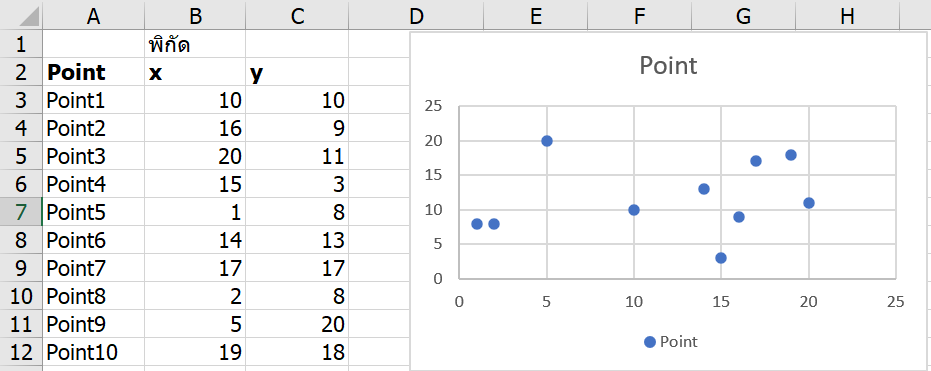
ในเมื่อเราต้องการระยะทางการวิ่งน้อยที่สุด ดังนั้นเราต้องคำนวณระยะทางระหว่างแต่ละจุดให้ได้ก่อน ซึ่งเราจะสร้างตารางที่ Cross กันระหว่างแต่ละจุดออกมาเพื่อสร้างความเป็นไปได้ทุกกรณี และใช้สูตรหาระยะทางระวห่างจุดโดยใช้ความสัมพันธ์ของสามเหลี่ยมมุมฉากดังนี้
ระยะทางระหว่างสองจุด (ด้านเฉียงของสามเหลี่ยมมุมฉาก)
=SQRT((X1-X2)^2+(Y1-Y2)^2)สรุปได้ดังนี้
=SQRT(($C18-F$15)^2+($D18-F$16)^2)
ทีนี้เพื่อป้องกันไม่ให้มันวิ่งจากจุดเดียวกันไปยังจุดเดียวกัน เราจะแก้สูตรให้ระยะห่างระหว่างจุดเดียวกันเป็นเลขเยอะๆ ไปเลยเช่น 9999 Solver มันจะได้ไม่เลือกเส้นทางนั้น
=IF(SQRT(($C18-F$15)^2+($D18-F$16)^2)=0,9999,SQRT(($C18-F$15)^2+($D18-F$16)^2))
ต่อไปเราจะสร้างการจัดสินใจ ว่าจะเลือกวิ่งเส้นทางไหน โดยการตัดสินใจให้เป็นเลข 0 (ไม่วิ่ง) ,1 (วิ่ง) และคำนวณผลรวมด้านขวาและด้านล่างออกมา จากนั้นคำนวณระยะทางรวมจากการใช้ SUMPRODUCT ปกติ

จากนั้นเรียกใช้ Solver โดย Min ระยะทางรวม และให้ Variable เป็น F32:O41 แล้วตั้งให้ Constrain เป็นแบบ Binary
นอกจากนั้นตั้ง Constrain
- ให้ผลรวมด้านขวาเป็น 1 ทั้งหมด (หมายถึงว่า ทุกจุดเป็นต้นทางแค่ 1 ครั้ง)
- ให้ผลรวมด้านล่างเป็น 1 ทั้งหมด (หมายถึง ทุกจุดเป็นปลายทางแค่ 1 ครั้ง)

พอ Solve ปุ๊ปมันจะได้แบบนี้

จะเห็นว่ามันทำการจับคู่ Point ที่อยู่ใกล้กัน แล้ววิ่งหากันเองซะงั้น (เช่น จาก 1->9 และ 9->1 ใหม่) เพราะเงื่อนไขที่เราตั้งไว้มันไม่ครอบคลุมว่าห้ามวิ่งกลับที่เดิมนั่นเอง
หากเราจะป้องกันไม่ให้เกิดเหตุการณ์ที่ไม่ต้องการ ก็ต้องใส่เงื่อนไขเพิ่มไปอีก เช่น เส้น1ไป9 + เส้น 9ไป1 ต้องได้ <=1 (คือห้ามเป็น 1 ทั้งคู่) พอ Solve ปุ๊ป Loop ปัญหานั้นๆ ที่เราดักไว้ก็จะหายไป
แต่เราต้องไปไล่กำจัด Loop ปัญหาอีกเรื่อยๆ จนหมด เช่น ถ้าเรากำกจัดวิ่งไปกลับของ 2 จุดได้ เราก็ต้องมาดักกรณีวิ่งไปกลับแบบ 3 จุดอีก เช่น จากรูป มันบอกว่าจาก 1->9 ->6 ->1 ใหม่ เราก็ต้องมาดักเงื่อนไขอีกว่า N32+K40+F37 <= 2 คือ ห้ามเป็น 1 ทั้ง 3 อัน เป็นต้น


เราต้องการทำให้วิ่งไปกลับครบ 10 จุด ห้ามมี Loop ย่อยๆ เลยแม้แต่ Loop เดียว แบบนี้ต้องเขียนเงื่อนไขดักเยอะมากๆๆ การมานั่งไล่ดัก Loop ปัญหา เป็นวิธีที่โหดร้ายเกินไป ดังนั้นเราจะเปลี่ยนแนวคิดไปแก้ด้วยวิธีอื่น
เปลี่ยนมุมมองการแก้ปัญหาไปใช้ All Different
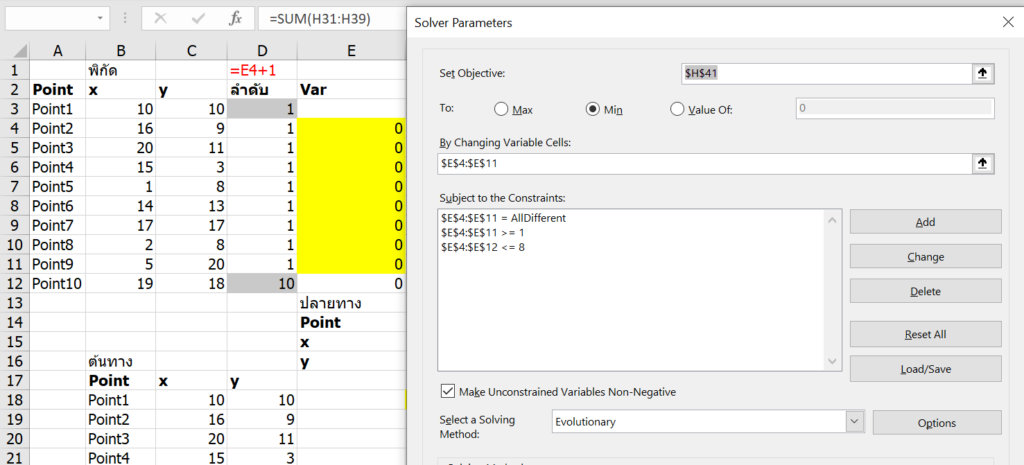
เราจะเปลี่ยนมุมมองการแก้ปัญหา ไปใช้การเลือกลำดับการวิ่ง 1-10 แทน โดยที่ลำดับนี้เป็นเลขแบบไม่ซ้ำกัน แล้วคำนวณมาว่าวิ่งลำดับใดจะให้ผลลัพธ์ที่ดีที่สุด ซึ่งความสัมพันธ์ของสูตรจะไม่ได้เป็นเส้นต่อเนื่องกันแล้ว จึงต้องใช้แบบ Evolutionary มาช่วย ควบคู่กับ Constrain แบบ All Different (ตัว Variable จะได้ค่าเป็น Integer ไม่ซ้ำกัน)
ดังนั้นเราจะแก้ Model ใหม่เป็นดังนี้ เราจะให้ Solver ใส่เลข 1-10 ลงไปในลำดับ (คอลัมน์ D) นี้

โดยที่เราเขียนสูตรรอไว้แล้วว่าพอมีเลข 1-10 แล้วระยะทางรวมจะเป็นเท่าไหร่

จากนั้นใน Solver ก็ตั้งค่าดังนี้
- หลักๆ คือให้ Variable >=1 และ <=10 และมีค่าต่างกันทั้งหมด (dif)
- ส่วน Solving Method ใช้ Evolutionary เพราะค่าจาก INDEX หรือการ Lookup มันกระโดดไปมาไม่ต่อเนื่องกันแน่นอน

ซึ่งพอ Solve แล้วมันจะคิดนานกว่า Simplex LP มากๆ เพราะมันต้องสุ่มตัวเลขใส่ลงไปจนกว่าจะได้คำตอบ (อันนี้ก็ต้องรอไปนะ…)

มันให้คำตอบออกมาว่า วิ่งจาก 9->6->7->10->3->2->4->1->8->5->9 ซึ่งจะมีระยะทางรวม 66.761
โดยมันขึ้นมาว่า
- Solver cannot improve the Current solution = ทำให้คำตอบดีขึ้นกว่านี้ไม่ได้ (ภายใต้เวลาที่กำหนด เช่น ภายใน Max Time without improvement ที่ตั้งไว้ มันหาตัวที่ดีขึ้นไม่ได้แล้ว)
- All Constraints are satisfied. = ทำตามเงื่อนไขได้ทั้งหมด
สังเกตว่ามันไม่ได้บอกว่าคำตอบที่ได้นั้น Optimal แค่บอกว่าทำให้ดีขึ้นไม่ได้แล้ว นั่นคือยังมีความเป็นไปได้ที่ผลลัพธ์ยังดีขึ้นได้กว่านี้อีก ซึ่งเราสามารถลองกด Solve ใหม่ได้เพื่อดูว่าค่าดีขึ้นหรือไม่ โดยอาจเปลี่ยน Mutation Rate ให้เยอะขึ้น ให้ Max Time มากขึ้น เป็นต้น
แต่ที่ผมลองเลขที่ได้ไม่เปลี่ยนจาก 66.761 แล้ว แต่อาจได้ค่าวนกลับอีกทางคือ
9->5->8->1->4->2->3->10->7->6->9 ซึ่งก็คือวงเดิมนี่แหละ แค่กลับอีกทาง

หากเราลองเอามา Plot กราฟ (Sort ตามลำดับที่ Solve ได้) ก็จะได้ดังนี้

สมมติว่ามีข้อกำหนดว่า ต้องเริ่มที่จุด 1 แล้วจบที่ จุด 10 แบบไม่ต้องวน
เราลองแก้ Model เล็กน้อย โดย Fix ลำดับ 1 กับ 10 เอาไว้เลย ดังนี้

แล้วเราก็ไปแก้ตอนคิดระยะทางว่าไม่ต้องวนกลับมาจุดแรก

จากนั้นการตั้งค่า Solver ก็ให้แก้เลขจาก 2-9 แทน และขอบเขตตัวแปรก็น้อยลงเป็นดังนี้
Tips : ถ้าไม่อยากมานั่งแก้ Range ก็สามารถใช้การตั้งชื่อ Defined Name มาช่วยได้ครับ

พอ Run แล้วปรากฏว่า Solver ไม่ยอมให้ AllDifferent มีค่าขอบเขต Lower โดยไม่ใช่ 1 และก็บอกว่าค่า Upper จะต้องเท่ากับจำนวน Variable เท่านั้น แปลว่าผมต้องใส่เป็นเลข 8

ดังนั้นผมจะแก้ Model อีกเล็กน้อย ให้มันใส่เลข 1-8 ก็ได้ แล้วผมค่อยบวก 1 ให้เป็น 2-9 อีกที

ซึ่งหากลองใส่เลข 1-10 ตามลำดับไปก่อน แล้วPlot กราฟ จะได้ระยะทางและรูปร่างการวิ่งดังนี้ อันนี้คือแบบไม่ได้วางแผนใดๆ ทำตามลำดับข้อมูลปกติ

ทีนี้เราจะลองหาว่าจะวิ่งยังไงให้ดีที่สุด?
พอกด Solve จะได้ดังนี้
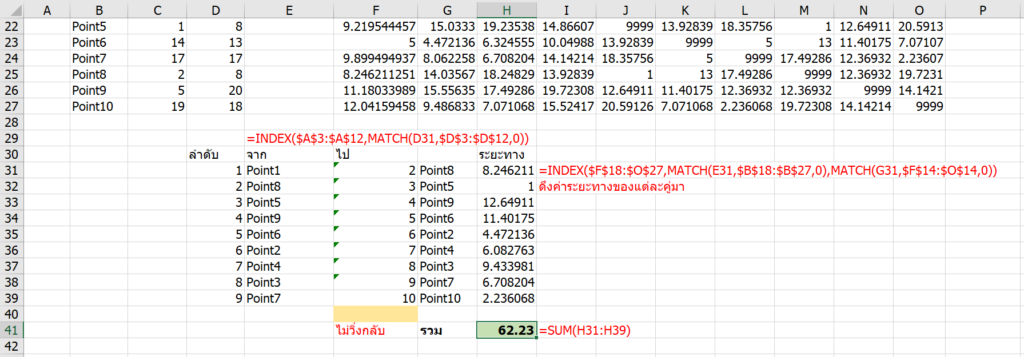
ซึ่งจะวิ่งจาก 1->8->5->9->6->2->4->3->7->10 นั่นเอง
หากเราลองเอามา Plot กราฟ (Sort ตามลำดับที่ Solve ได้) ก็จะได้ดังนี้
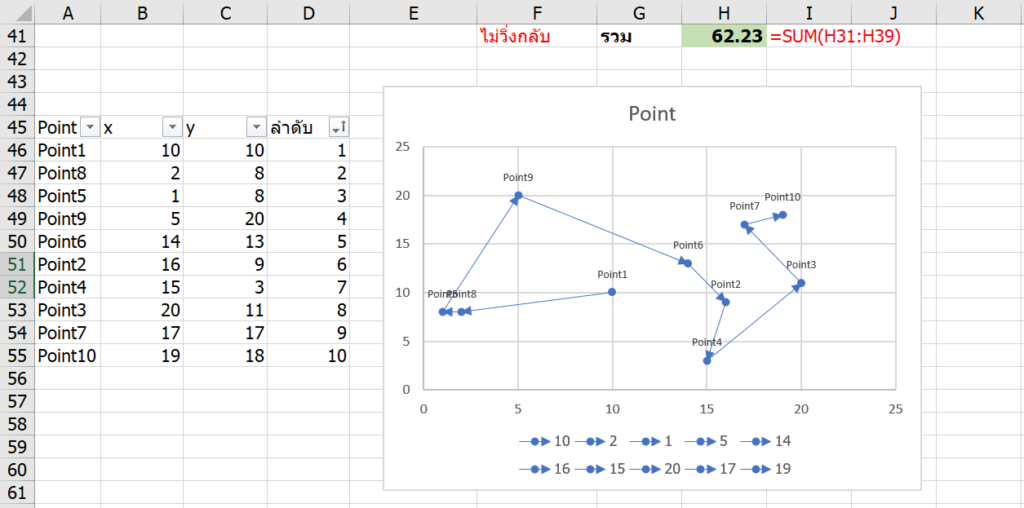
ส่วนถ้าใครอยากรู้ว่า วิ่งยังไงให้เปลืองระยะทางมากที่่สุด ก็จะลองปรับค่า Objective เป็น Max ดูได้ครับ ผลที่ได้จะทุเรศมากดังนี้ 555

ตัวอย่าง 5 : Optimize การตัดแบ่งวัตถุดิบ
โจทย์คือ เราซื้อวัตถุดิบมาแบบชิ้นใหญ่ แล้วต้องเอามาตัดแบ่งเพื่อผลิตสินค้าตามที่กำหนด เราต้องหาวิธีตัดให้มีประสิทธิภาพมากสุด (โจทย์แบบนี้เค้าเรียกกันว่า Cutting stock problem ครับ)
ตัวอย่างนี้ผมเคยเขียนบทความและทำเป็นคลิปไว้ให้แล้ว เป็นเนื้อหาที่ค่อนข้าง Advance (มีการใช้ Power Query ช่วยด้วย) ใครสนใจสามารถดูคลิปได้เลย (เคยทำไว้นานแล้วแทบไม่มีคนดู 555)
สรุป
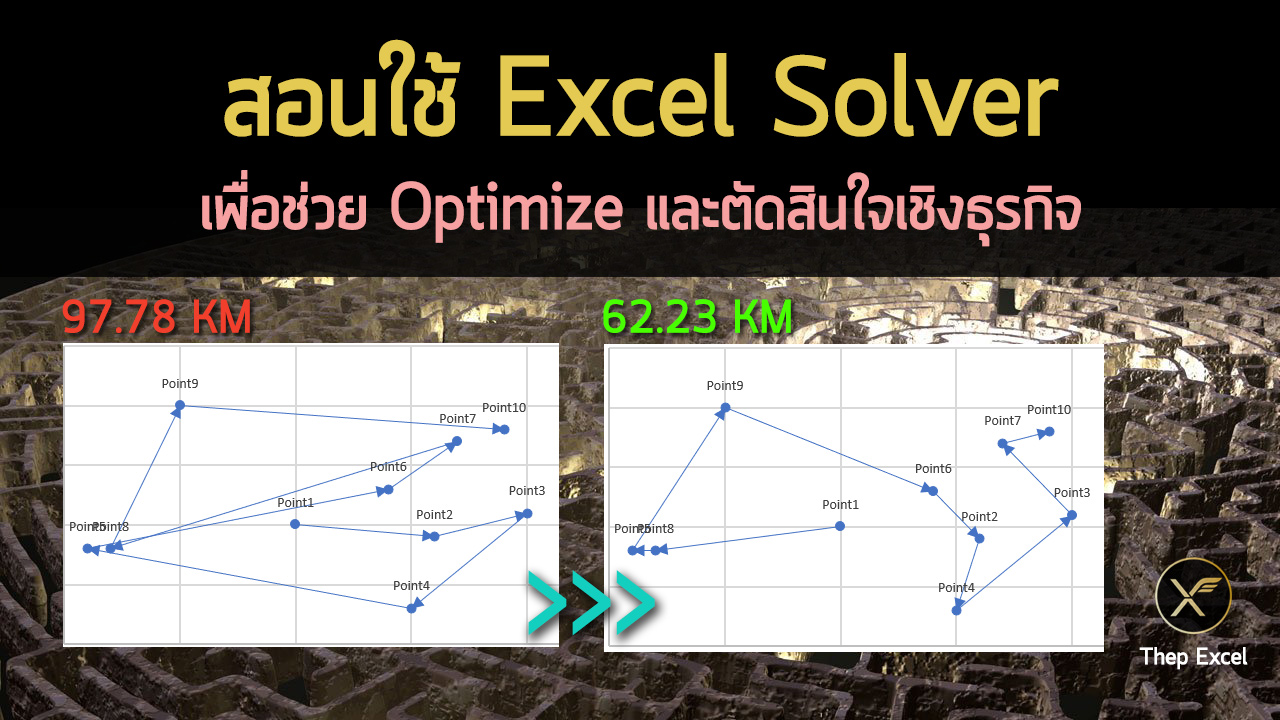
จากตัวอย่าง 4 (การวิ่งรถ) จะเห็นได้ชัดเลยว่าการวางแผนที่ดี จะช่วยให้ระยะทางที่วิ่งรถน้อยลงไปมาก จากที่ไม่วางแผนเลยต้องวิ่งระยะ 97.78 แต่ถ้าวางแผนให้วิ่งน้อยสุดจะวิ่งแค่ 62.23 เท่านั้น (ประหยัดขึ้นถึง 37%) ส่วนถ้าตั้งใจวิ่งให้ยาวที่สุด จะยาวถึง134.93 (ซึ่งยาวขึ้นจาก Base 37% )
ดังนั้นคุณอยากให้ค่าใช้จ่ายน้อยลง แต่ได้ผลลัพธ์เท่าเดิม ก็อย่าลืม Optimize ธุรกิจของคุณด้วยนะครับ ^^
ใครสนใจเรื่อง Solver โดยละเอียด สามารถศึกษาได้จากคอร์สออนไลน์ที่ผมทำไว้อันนี้ได้ครับ
คอร์สออนไลน์ การทำ Optimization ด้วย Excel Solver สำหรับงานวางแผน

คุณกำลังมองหาวิธีพัฒนาทักษะ Excel ของคุณไปสู่อีกระดับหรือไม่ ?
คุณต้องการแก้ปัญหาที่ซับซ้อนและตัดสินใจให้ดีมากขึ้นในธุรกิจ ชีวิตส่วนตัว หรือการเรียนหรือไม่ ?
คำตอบอยู่ที่นี่แล้ว! เพราะหลักสูตรนี้ คือหลักสูตรที่ครอบคลุมการเรียนรู้ในการเพิ่มประสิทธิภาพและค้นหาวิธีแก้ปัญหาที่ดีที่สุดสำหรับปัญหาต่าง ๆ (Optimization) โดยใช้เครื่องมือ Excel Solver ที่มีอยู่แล้วใน Excel ทุก Version
ประโยชน์ที่จะได้จากคอร์สนี้
- ทำความเข้าใจอย่างลึกซึ้งเกี่ยวกับ Excel Solver และการนำไปใช้ในสถานการณ์ต่าง ๆ ผ่านตัวอย่างกรณีศึกษาที่หลากหลาย เช่น
– การวางแผนการผลิตสินค้า
– การจัดสรรพนักงานให้เป็นไปตามเป้าหมาย
– การจัดสรรเวลาให้มีประสิทธิภาพสูงสุด
– การใช้ Budget ให้คุ้มค่าที่สุด แบบมีเงื่อนไขซับซ้อน
– การวางแผนการลงทุน
– การวางแผนการลงทุนสร้างโรงงาน
– ส่งของจากศูนย์กระจายสินค้าให้ต้นทุนต่ำที่สุด
– การหาเส้นทางที่สั้นที่สุด (Shortest Path)
– การวางแผนลำดับเส้นทางการเดินทาง (Traveling Salesman)
– การเปลี่ยนเครื่องจักรให้คุ้มค่า
– การวางแผนในเชิงการหาตำแหน่งที่เหมาะสมในเชิงพื้นที่ (Set Covering) - ทำความเข้าใจวิธีจัดลำดับความสำคัญของวัตถุประสงค์หลายรายการและค้นหาวิธีแก้ปัญหาที่ดีที่สุด
- เพิ่มทักษะ Excel ของคุณและปรับปรุงความสามารถในการตัดสินใจของคุณ
- เพิ่มคุณค่าให้ตัวคุณได้อย่างมหาศาล เพราะการ Optimize ทางธุรกิจสามารถสร้างผลกำไรเพิ่มให้องค์กรได้จริง
- เพิ่มความโดดเด่นในใบสมัครงานของคุณ ด้วยการเพิ่มทักษะที่โดดเด่น และหายากในตลาดแรงงานไทย





Leave a Reply